Bloom's 2 sigma problem
Tutoring is super effective, but how can we achieve its effects at scale?
Bloom’s 2 sigma problem is the following: one-on-one tutoring is basically the most effective way of teaching, but it’s obviously difficult to scale, so what can we do instead? In this post, I’ll summarize the solutions outlined in Benjamin Bloom’s 1984 survey and end with a few thoughts on how these might apply to college.
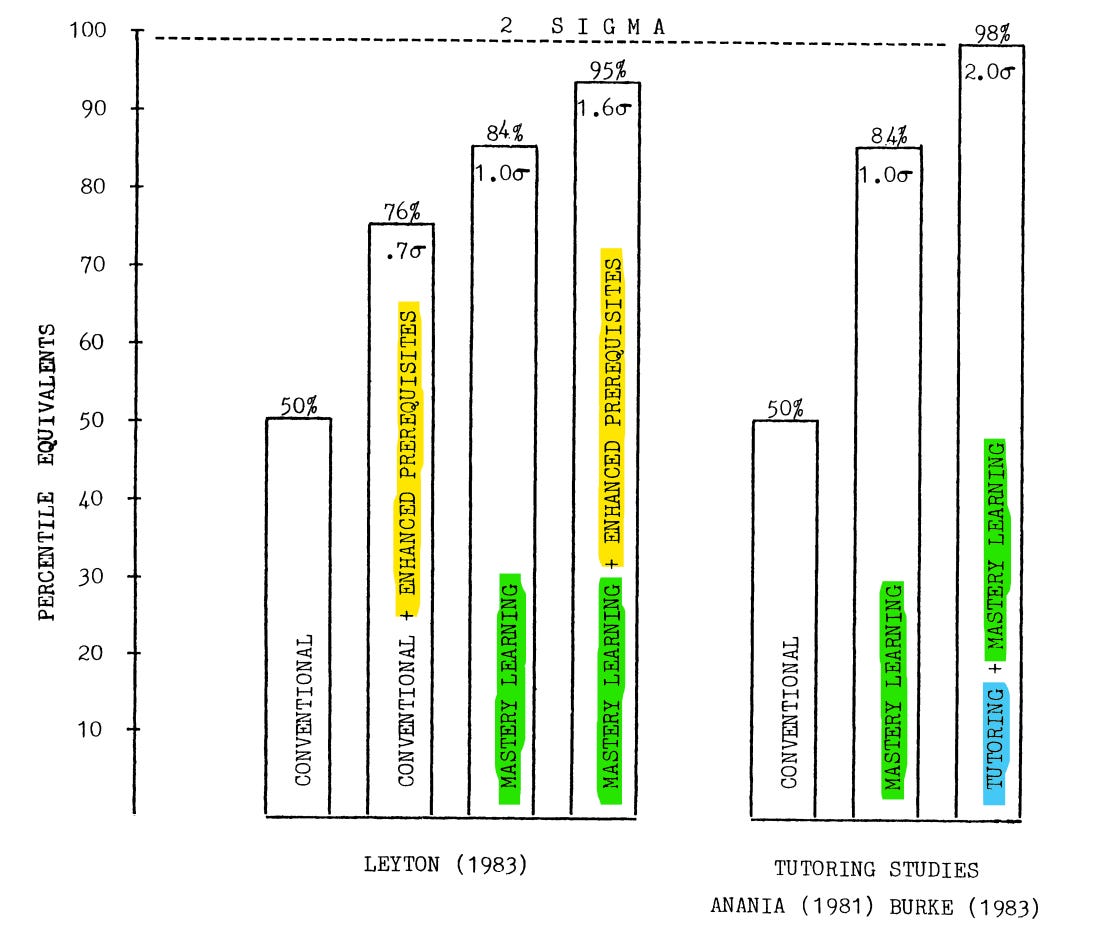
Before we begin: the “2 sigma” refers to the effect size of tutoring. In his paper, Bloom repeatedly reminds us that the average tutored student performs 2 standard deviations better than the average non-tutored student. In other words, they’re above 98% of the control group. That’s huge!
Mastery Learning (ML): 1 sigma
Let’s start with Mastery Learning (ML); as we’ll see later, Bloom is a fan of sprinkling it on top of other techniques. In ML, students don’t move on to Unit 2 until they have mastered Unit 1. This means that within the same class, different students work on different things, depending on how much each student has mastered. ML involves a lot of testing and feedback that helps the teacher effectively guide students on their individual journeys toward mastery. Bloom claims that ML alone yields a 1 sigma improvement.
Enhanced Prerequisites + ML: 1.6 sigma
Enhancing prerequisites is the extension of ML to the beginning of the semester. Right before starting Algebra 2 or French 2, teachers can spend a few hours on testing and reviewing the content from Algebra 1 or French 1. This is a small, short-term cost with a scalable, long-term benefit: enhancing prerequisites alone provides a 0.7 sigma improvement, and when combined with ML, we get 1.6 sigma.
Improved Instructional Materials: 0.2 sigma
The effect size of this one is relatively small, but at least it’s highly scalable. Bloom claims that most improvements to textbooks (e.g., better illustrations) don’t actually help student achievement. Instead, he’s interested in creating and equipping students with “organizers” that provide, at the beginning of a chapter, the main ideas of that chapter and how it connects to other chapters. This improves achievement by 0.2 sigma and retention by 0.4 sigma.
Home/Peer Environment: 1 sigma
Bloom cites a study that found that having parents regularly meet with educators improved student achievement by 1 sigma. I won’t elaborate on this since it’s virtually impossible for college educators. Students’ peers also matter, and Bloom thinks the availability of clubs could “enable students to be more selective in their peer choices.”
Reaching More Students: 1.5-1.7 sigma
Teachers generally pay the most attention to the top third of the class and the least attention to the bottom third, despite their impression that they treat all students equally. (In contrast, a private tutor pays all of their attention to the tutee, who gets tons of feedback on their progress.) So in one study, the researchers helped teachers provide better cues (positive feedback) and explanations to students, and increase students’ active participation; this resulted in a 1.5 sigma improvement. A later study showed that combining the enhanced cues, participation, and reinforcement approach with ML increases the improvement to 1.7 sigma. Bloom concludes this section by emphasizing the importance of teachers being made aware of their styles of interaction through feedback from students, observers, or even video recordings.
Higher Mental Processes: 1.3-2 sigma
I found this one to be the most handwavy, but it’s the only non-tutoring variable that yields a 2 sigma improvement (in some sense). Basically, some schools in some countries (Bloom cites Israel, Malaysia, and South Korea) emphasize “problem-solving, application of principles, analytical skills, and creativity,” while schools in the US focus on specific content and “tests of remembered information.”1 Here's a passage about how subjects are taught "as methods of inquiry" in the first group of schools:
The subjects are taught as much for the ways of thinking they represent as for their traditional content. Much of this learning makes use of observations, reflections on these observations, experimentation with phenomena, and the use of first hand data and daily experiences, as well as the use of primary printed sources.
One study sought to improve students’ achievement with respect to higher mental processes by emphasizing heuristic problem solving and including both higher and lower mental process questions in tests and feedback (as well as ML). This group did 1.3 sigma better than the one that primarily focused on learning algorithms. Another study used ML and asked students to apply principles in a variety of contexts, and when researchers measured students’ ability to apply these principles to a new problem, they found a 2 sigma improvement over students who learned the principles without the applications.
Takeaways
For college instruction, I think all of the points make sense except for home/peer environment variables. Better prerequisite preparation (e.g., review CS1 before CS2, discrete math before algorithms), teaching resources, interactions with the whole class, and incorporation of higher mental processes all sound like good (but potentially vague and lofty) goals.
And let’s not forget about Mastery Learning: it sounds great to me, but it certainly doesn’t sound easy to implement. The most scalable solution is probably something like Khan Academy: a high-tech, guided, private tour accompanied by a personal practice regimen. But having students sit in front of their laptops rubs against the spirit of the traditional college experience (with in-person lectures, discussions, etc.), which I think is valuable. Surely there’s some hybrid experience that gets the best of both worlds.
This is a bit funny to me since we (Americans) have heard things like, “Our schools are better than other countries’ schools because we, unlike them, focus on critical thinking and creativity rather than rote memorization.” At the same time, many (including teachers) are not thrilled with our education system.

